【青果×ポケモン】シンオウ地方ポケモンに青果商品のニックネームをつける

タイトルでわかるとおり、ネタ回です。

はじめに

スーパーは好きですか。僕は好きです。
コンビニは割高なので、原則スーパーでしか買い物をしません。
また、超(スーパー)アルバイターとして約4年ほど働き、精肉、鮮魚、青果と渡り歩いてきました。

ポケモンは好きですか。僕は好きです。
11月19日発売のダイパリメイクに向け、旅パを考えるくらいには発売を楽しみにしています（パール購入予定）。
旅パは固まりつつも、旅をしていく上で、もう一つ重要な要素があります。
そうです。ニックネームです。
ニックネームをつけなければ愛着というものが欠如してしまいます。
つまり、旅パのポケモンたちを超(スーパー)ポケモンにするためにも、ポケモンたちに超(スーパー)な、名前をつけなければなりません。

今回は、僕が超(スーパー)アルバイターとして最後の一年半働いていた青果をテーマに、ポケモンたちのニックネームを決めていきたいと思います。

タスク

超(スーパー)意味分かんないと思うので、何するのかを具体的に説明します。
ポケモンのニックネームを青果にある商品（野菜、果物、花等）から決めます。
青果にある商品の画像を適当に集め、分類器を作成します。その分類器からポケモンの画像がどの青果にある商品に分類されるかで、ニックネームもとを決めます。
そんなん草ポケモンしか意味ないやん。そんな声が聞こえます。僕もそう思います。

※ちなみに御三家はポッチャマで決定なのですが、ニックネームは【すだち】で決定しております。
異論は認めません！

データセット

ポケモンの画像

既存の全ポケモンの画像がありますが、ナエトル~アルセウスまでのシンオウ地方だけに抽出します。

Pokemon Images Datasetwww.kaggle.com

花

• daisy：ヒナギク
• dandelinon：タンポポ
• rose：バラ
• sunflower：ヒマワリ
• tulip：チューリップ

花はもう少し種類が欲しかったですが、仕方ないですね……。

Flowers Recognitionwww.kaggle.com

野菜と果物

種類が多いので、どんな野菜や果物があるかは、リンク先を参照してください。

また、このデータセットに関してはいくつか変更点があります。

1. データセットが怪しい 例えばAppleの中にりんごの画像ではなく、某社のロゴや商品があったりしました。

2. データセットの枚数が不十分 このデータセットの種類が一番多いのですが、100枚ずつと見せかけて、100枚足りないものがありました。

これらはどちらも、自分でダウンロードした別の画像を加えています。
なお、今回の画像データセットに【すだち】はないです。

Fruit and Vegetable Image Recognitionwww.kaggle.com

プログラム

データセット作成

関数定義します。気合と根性のsplitは察してください。

import os
import pickle
import glob as gb
import pandas as pd
import numpy as np
import cv2
import matplotlib.pyplot as plt
import re
from tensorflow.keras.preprocessing.image import ImageDataGenerator, load_img, save_img, img_to_array, array_to_img


# シンホウ地方だけに抽出
def extract_sinnoh(pokemon_path_list):
    """
    387~493
    ナエトル~アルセウス
    """
    sinnoh_pokemon_path_list = []
    for pokemon in pokemon_path_list:
        # print(pokemon)

        # 数字だけにファイル名を頑張って除去
        number = int(re.sub(r'[f]', '', (pokemon.split('\\')[1].split('.')[0].split('-')[0])))
        
        # シンホウ地方
        if number >= 387 and number <= 493:
            # print(number)
            sinnoh_pokemon_path_list.append(pokemon)

    return np.array(sinnoh_pokemon_path_list)


# 画像読込
def load_images(image_path_list, pokemon=False, show=False):
    npy_image_list = []

    for i, image in enumerate(image_path_list):
        image_path = image.replace(chr(92), '/') # \を/に置換(windows特有)->macはchr(165)
        if i % 100 == 0: # 雑に進行状況出力
            print(i)

        # 読み込み
        img = load_img(image_path, grayscale=False, color_mode='rgb', target_size=(128,128))
        img_npy = img_to_array(img)

        if pokemon:
            index = np.where(img_npy[:, :, 2] == 0)
            img_npy[index] = [255, 255, 255] # 透過を白塗り

        img_npy = img_npy / 255 # 正規化

        if show:
            print(img_npy.shape)
            plt.imshow(img_npy)
            plt.show()
            break

        npy_image_list.append(img_npy)

    return np.array(npy_image_list)


# npy形式で保存
def save_npy_image(save_path, images):
    np.save(save_path, images)
    print('save ', save_path)

シンオウ地方だけのポケモンを抽出しnpy形式で保存。
npy形式で保存し直しているのは、学習するのに大量の画像を読み込むとメモリ不足で死ぬからです。

# 読込
pokemon_path_list = gb.glob('D:/OpenData/pokemon_dataset/Pokemon-Images-Dataset/pokemon/*')
sinnoh_pokemon_path_list = extract_sinnoh(pokemon_path_list)

# 抽出
pokemon_image_list = load_images(sinnoh_pokemon_path_list, pokemon=True, show=False)

# 保存
save_npy_image('D:/OpenData/pokemon_dataset/Pokemon-Images-Dataset/npy/pokemon_sinnoh_128.npy', pokemon_image_list)

花の画像5種類を読み込みnpy形式で保存。

# 読込
daisy_path_list = gb.glob('D:/OpenData/flowers/raw/daisy/*')
dandelion_path_list = gb.glob('D:/OpenData/flowers/raw/dandelion/*')
rose_path_list = gb.glob('D:/OpenData/flowers/raw/rose/*')
sunflower_path_list = gb.glob('D:/OpenData/flowers/raw/sunflower/*')
tulip_path_list = gb.glob('D:/OpenData/flowers/raw/tulip/*')

# daisy_image_list = load_images(daisy_path_list, show=True)
# dandelion_image_list = load_images(dandelion_path_list, show=True)
# rose_image_list = load_images(rose_path_list, show=True)
# sunflower_image_list = load_images(sunflower_path_list, show=True)
# tulip_image_list = load_images(tulip_path_list, show=True)

# 保存
save_npy_image('D:/OpenData/flowers/npy/daisy_128.npy', daisy_image_list)
save_npy_image('D:/OpenData/flowers/npy/dandelion_128.npy', dandelion_image_list)
save_npy_image('D:/OpenData/flowers/npy/rose_128.npy', rose_image_list)
save_npy_image('D:/OpenData/flowers/npy/sunflower_128.npy', sunflower_image_list)
save_npy_image('D:/OpenData/flowers/npy/tulip_128.npy', tulip_image_list)

野菜と果物を読み込みnpy形式で保存。

# 読込
fruit_vegetable_path_list = gb.glob('D:/OpenData/Fruit-and-Vegetable-Image-Recognition/train/*/*') 
fruit_vegetable_image_list = load_images(fruit_vegetable_path_list, show=False)

# 保存
save_npy_image('D:/OpenData/Fruit-and-Vegetable-Image-Recognition/npy/fruit_vegetable_128.npy', fruit_vegetable_image_list)

学習・予測

こちらは過去に書いたコードをほぼそのまま引っ張ってきてます。

noleff.hatenablog.com

まずは学習するためのデータを準備をします。

def load_npy_image(load_path):
    return np.load(load_path, allow_pickle=True)

## 読込
# 花
daisy = load_npy_image('D:/OpenData/flowers/npy/daisy_128.npy')
dandelion = load_npy_image('D:/OpenData/flowers/npy/dandelion_128.npy')
rose = load_npy_image('D:/OpenData/flowers/npy/rose_128.npy')
sunflower = load_npy_image('D:/OpenData/flowers/npy/sunflower_128.npy')
tulip = load_npy_image('D:/OpenData/flowers/npy/tulip_128.npy')

# 果物と野菜
fruit_vegetable = load_npy_image('D:/OpenData/Fruit-and-Vegetable-Image-Recognition/npy/fruit_vegetable_128.npy')


## ラベル
# 花
flowers_labels = [re.split('[\\\.]',path)[-1] for path in gb.glob('D:/OpenData/flowers/raw/*')]

# 果物と野菜
fruit_vegetable_labels = [re.split('[\\\.]',path)[-1] for path in gb.glob('D:/OpenData/Fruit-and-Vegetable-Image-Recognition/train/*')]

labels = flowers_labels + fruit_vegetable_labels # ファイル名をだけを抽出してlabelsに入れてます。

データセットを作ります。

def make_dataset(daisy, dandelion, rose, sunflower, tulip, fruit_vegetable, fruit_vegetable_labels):
    # 画像
    flowers = np.concatenate([daisy, dandelion], axis=0)
    flowers = np.concatenate([flowers, rose], axis=0)
    flowers = np.concatenate([flowers, sunflower], axis=0)
    flowers = np.concatenate([flowers, tulip], axis=0)
    X = np.concatenate([flowers, fruit_vegetable], axis=0)

    # ラベル
    labels = [0] * len(daisy) + [1] * len(dandelion) + [2] * len(rose) + [3] * len(sunflower) + [4] * len(tulip) # flowers label
    for i in range(len(fruit_vegetable_labels)):
        labels += [i+5] * 100  # 各画像ごとに100枚ずつ
    y = np.array(labels)

    return X, y


X, y = make_dataset(daisy, dandelion, rose, sunflower, tulip, fruit_vegetable, fruit_vegetable_labels)
X_train, X_val, y_train, y_val = train_test_split(X, y, test_size=0.20, shuffle=True, random_state=2021)

学習です。keras使ってCNNぶん回します。

import tensorflow.keras as keras
from tensorflow.keras.models import Sequential, Model, load_model
from tensorflow.keras.layers import AveragePooling2D, Dense, Conv2D, MaxPooling2D, Flatten, Input, Activation, add, Add, Dropout, BatchNormalization
from tensorflow.keras.optimizers import SGD
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.utils import to_categorical

from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, confusion_matrix,  accuracy_score, recall_score, precision_score, f1_score
from sklearn.model_selection import StratifiedKFold
from tensorflow.keras.applications import InceptionV3
from tensorflow.keras.preprocessing.image import ImageDataGenerator, load_img, save_img, img_to_array, array_to_img 

# モデル構築
def build_inception_model(out_shape):
    base_model = InceptionV3(weights='imagenet', 
                            include_top=False, 
                            input_tensor=Input(shape=(128, 128, 3)))
    x = base_model.output
    x = AveragePooling2D(pool_size=(2, 2))(x)
    x = Dropout(.4)(x)
    x = Flatten()(x)
    predictions = Dense(out_shape, activation='softmax')(x)

    model = Model(base_model.input, predictions)

    opt = SGD(lr=.01, momentum=.9)
    model.compile(optimizer=opt, loss='categorical_crossentropy', metrics=['accuracy'])

    model.summary()

    return model

def build_base_model(out_shape):
    '''
    初期化 (initializer)
    Glorotの初期化法:sigmoid関数やtanh関数
    Heの初期化法:ReLU関数
    https://ichi.pro/zukai-10-ko-no-cnn-a-kitekucha-164752979288397
    '''
    model = Sequential()

    # 入力画像 128x128x3 (縦の画素数)x(横の画素数)x(チャンネル数)
    model.add(Conv2D(16, kernel_size=(5, 5), activation='relu', kernel_initializer='he_normal', input_shape=(128, 128, 3)))
    model.add(MaxPooling2D(pool_size=(3, 3)))
    model.add(Conv2D(64, kernel_size=(5, 5), activation='relu', kernel_initializer='he_normal'))
    model.add(MaxPooling2D(pool_size=(3, 3)))
    model.add(Conv2D(256, kernel_size=(3, 3), activation='relu', kernel_initializer='he_normal'))
    model.add(MaxPooling2D(pool_size=(2, 2)))
    model.add(Dropout(0.4))

    model.add(Flatten())
    model.add(Dense(2560, activation='relu',kernel_initializer='he_normal'))
    model.add(Dropout(0.2))  
    model.add(Dense(640, activation='relu', kernel_initializer='he_normal'))  
    model.add(Dense(128, activation='relu', kernel_initializer='he_normal')) 
    model.add(Dropout(0.2))
    model.add(Dense(out_shape, activation='softmax'))

    model.compile(
        loss='categorical_crossentropy',
        optimizer='adam',
        metrics=['accuracy']
    )

    model.summary()

    return model

# 画像の水増し
def make_datagen(rr=30, wsr=0.1, hsr=0.1, zr=0.2, val_spilit=0.2, hf=True, vf=True):
    datagen = ImageDataGenerator(
            # https://keras.io/ja/preprocessing/image/
            # rescale = 1./255,                      # スケーリング　
            featurewise_center = False,            # データセット全体で，入力の平均を0にするかどうか
            samplewise_center = False,             # 各サンプルの平均を0にするかどうか
            featurewise_std_normalization = False, # 入力をデータセットの標準偏差で正規化するかどうか
            samplewise_std_normalization = False,  # 各入力をその標準偏差で正規化するかどうか
            zca_whitening = False,                 # ZCA白色化を適用するかどうか
            rotation_range = rr,                   # ランダムに±指定した角度の範囲で回転 
            width_shift_range = wsr,               # ランダムに±指定した横幅に対する割合の範囲で左右方向移動
            height_shift_range = hsr,              # ランダムに±指定した縦幅に対する割合の範囲で左右方向移動
            zoom_range = zr,                       # 浮動小数点数または[lower，upper]．ランダムにズームする範囲．浮動小数点数が与えられた場合，[lower, upper] = [1-zoom_range, 1+zoom_range]です．
            horizontal_flip = hf,                  # 水平方向に入力をランダムに反転するかどうか
            vertical_flip = vf,                    # 垂直方向に入力をランダムに反転するかどうか
            validation_split = val_spilit          # 検証のために予約しておく画像の割合（厳密には0から1の間）
        )
    
    return datagen

# 学習
def learn_model(model, X_train, y_train, X_val=None, y_val=None):
    tr_datagen = make_datagen()       # 学習データだけ水増し
    va_datagen = ImageDataGenerator() # 検証データは水増ししない

    early_stopping = EarlyStopping(monitor='val_loss',
                                min_delta=1.0e-3, 
                                patience=20, 
                                verbose=1)

    if X_val is None:
        hist = model.fit_generator(tr_datagen.flow(X_train, y_train, batch_size=32), 
                                verbose=2, 
                                steps_per_epoch=X_train.shape[0] // 32,
                                epochs=100, 
                            )
    else:
        hist = model.fit_generator(tr_datagen.flow(X_train, y_train, batch_size=32), 
                                verbose=2, 
                                steps_per_epoch=X_train.shape[0] // 32,
                                epochs=100, 
                                validation_data=(X_val, y_val), 
                                callbacks=[early_stopping]    
                            )                
    return hist

# 予測
def predict_model(model, X_test):
    y_pred = model.predict(X_test, batch_size=128)

    return y_pred


# ラベルをOne-Hotに変換
y_onehot_train = to_categorical(y_train)
y_onehot_val = to_categorical(y_val)

# 学習
model_base = build_base_model(len(labels))
hist_base = learn_model(model_base, X_train, y_onehot_train, X_val, y_onehot_val)

model_inception = build_inception_model(len(labels))
hist_incepiton = learn_model(model_inception, X_train, y_onehot_train, X_val, y_onehot_val)

# モデル保存
model_base.save('../model/base.h5')
model_inception.save('../model/inception.h5')

続いて予測します。

# モデル読込
model_base = load_model('../model/base.h5')
model_inception = load_model('../model/inception.h5')

# 予測
pred_base = predict_model(model_base, pokemon)
pred_inception = predict_model(model_inception, pokemon)
pred_base = np.argmax(pred_base, axis=1)
pred_inception = np.argmax(pred_inception, axis=1)

結果をデータフレーム形式でまとめ、CSVで保存します。

# シンホウ地方だけに抽出
def extract_sinnoh(pokemon_path_list):
    """
    387~493
    ナエトル~アルセウス
    """
    sinnoh_pokemon_list = []
    for pokemon in pokemon_path_list:
        # print(pokemon)

        # 数字だけにファイル名を頑張って除去
        number = int(re.sub(r'[f]', '', (pokemon.split('\\')[1].split('.')[0].split('-')[0])))
        pokemon = re.sub(r'[f]', '', (pokemon.split('\\')[1].split('.')[0])) # ここだけ加筆
        
        # シンホウ地方
        if number >= 387 and number <= 493:
            # print(number)
            sinnoh_pokemon_list.append(pokemon)

    return np.array(sinnoh_pokemon_list)


# シンオウ地方のポケモンのファイル名を抽出
pokemon_path_list = gb.glob('D:/OpenData/pokemon_dataset/Pokemon-Images-Dataset/pokemon/*')
sinnoh_pokemon_list = extract_sinnoh(pokemon_path_list)

# 予測結果をCSVで保存
pokemon_df = pd.DataFrame()
pokemon_df['sinnoh_pokemon'] = sinnoh_pokemon_list
pokemon_df['pred_base'] = pred_base
pokemon_df['pred_inception'] = pred_inception

pokemon_df.to_csv('../data/result.csv', index=False)

予測精度

• base_model

• inception_model

ポケモンが何に分類されたか抜粋

愛しのポッチャマがバナナという結果になりました。
どこがバナナだったんでしょうか。くちばしですかね。
ともあれ、先んじて【すだち】宣言して正解？です。

base_model	inception_model	pokemon
sunflower	banana	ナエトル
soy beans	rose	ヒコザル
banana	banana	ポッチャマ
rose	rose	ロズレイド
beetroot	raddish	チェリム(ネガフォルム)
tulip	raddish	チェリム(ポジフォルム)
tulip	tulip	ロトム(ノーマルフォルム)
ginger	rose	ユクシー
rose	paprika	エムリット
daisy	daisy	アグノム
rose	daisy	ディアルガ
ginger	rose	パルキア

まとめ

青果にある商品の画像データをもとに分類器を作り、ポケモンの画像で予測させてみました。
結果はいかがだったでしょうか。
おそらく、全シンオウ地方ポケモンの内、ロズレイドしか納得できないですね、はい。

ネットワークサービスにおける任天堂の著作物の利用に関するガイドライン｜任天堂

ご利用について｜ポケットモンスターオフィシャルサイト

スライディングウィンドウ処理をしたIMUセンサデータに対して、クラスタリングによるパターン抽出は有効か否か

はじめに

以前、Twitterにて

前略ーー時系列データをsliding windowで切り取ってkmeansしてパターン見つけるみたいな手法あるけどそれやると正弦波になって意味ないでみたいな話を思い出したーー後略

というものを見かけました。

時系列データの前処理として、スライディングウィンドウ処理で部分時系列を作り、それを特徴ベクトルとして機械学習で予測する、みたいなことは何度も経験があるので、k-meansの中心点が正弦波（位相は問わない？）になるというのはとても興味深いです。
ツイートを見かけたときは「へー」くらいに思って、いいねしてたのですが、今回は気になったので、自分の持っているデータで調べてみることにしました。
文献としては少し古いですが、色々試してみようと思います。

データ

データは自転車の走行データを用います。
これはスマホでデータ収集しているのですが、自転車のかごに設置しております。
ポーチの中にスマホ入れております（迷彩柄のポーチは無視してください）。

具体的なデータは、IMU（加速度、ジャイロ、磁気センサ）のそれぞれXYZ、合計9軸で試してみます。
走行場所の詳細は言えませんが、私の自宅から大学間の約5kmになります。

プログラム

データ準備

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler

df = pd.read_csv('2021-09-02 09.csv')
df

下記がデータのサンプルです。
緯度経度などもとれますが、今回はこれらの時間（Time）を除くこれらのデータだけ試します。

Time	Acc_X	Acc_Y	Acc_Z	Roll	Pitch	Yaw	Com_X	Com_Y	Com_Z
2021-09-02 09:38:15	-0.188782	-0.530762	-0.850571	-0.295878	0.562196	1.688278	-2.819519	-11.504997	-10.297852

センサは先に述べたとおり、以下のものを使います。
また、文献の通り、k=3、window=128で以降を実装していきます。

sensors = [
    'Acc_X', 'Acc_Y', 'Acc_Z',
    'Roll', 'Pitch', 'Yaw',
    'Com_X', 'Com_Y', 'Com_Z'
]

k = 3
window = 128

まず、全体の可視化を見てみましょう。

for sensor in sensors:
    plt.figure(figsize=(20,4))
    plt.title(sensor)
    plt.plot(df[sensor])
    plt.show()

クラスタリング(k-means)するので、標準化しておきます。
スケーリング大事。

def scaler(df, sensors):
    scaler = StandardScaler()
    arr = scaler.fit_transform(df[sensors])
    df_std = pd.DataFrame(arr, columns=sensors)
    return df_std

df_std = scaler(df, sensors)

部分時系列を作成します。
文献と同じくウィンドウサイズ128とし、1ステップずつwindowをずらしていきます。

def make_subsequences(df, sensor):
    vec = df[sensor].values
    return np.array([vec[i:i+window] for i in range(len(vec)-window+1)])

部分時系列の初めだけを可視化するのと、以下のようになります。

for sensor in sensors:
    plt.figure(figsize=(20,4))
    plt.title(sensor)
    subsequences = make_subsequences(df_std, sensor, window)
    plt.plot(subsequences[0])
    plt.show()

クラスタリング

いよいよ本番です。
文献の通りk=3としてクラスタリングをし、中心点をクラスタごとに色分けして可視化してみます。
なお、中心点のデータサイズが異なるため、可視化用にスケーリングしてます（可視化結果を見やすくするためです）。

kmeans = KMeans(n_clusters=k, random_state=2021)
scaler = StandardScaler()

for sensor in sensors:
    subsequences = make_subsequences(df_std, sensor, window)
    kmeans.fit_predict(subsequences)
    centers = scaler.fit_transform(kmeans.cluster_centers_)

    plt.figure(figsize=(20,4))
    plt.title(sensor)
    plt.plot(centers[0], label='cluster1')
    plt.plot(centers[1], label='cluster2')
    plt.plot(centers[2], label='cluster3')
    plt.legend(loc='upper right')
    plt.show()

結果

結果をまとめると以下のような感じでしょうか。
完全主観にはなりますが、Acc_XやRollはかなり正弦波ぽいですね。

sensor	result
Acc_X	正弦波ぽい
Acc_Y	あやしい
Acc_Z	あやしい
Roll	正弦波ぽい
Pitch	平ら
Yaw	平ら
Com_X	正弦波ぽい
Com_Y	正弦波ぽい
Com_Z	平ら

データ数増やして再チャレンジ

往々にして、データサイエンス分野はデータない問題とデータ足りない問題が、結果の原因となります。
今回は、データはそこそこ持っているので、脳筋戦法ということで増やしてみました。

• Before

  • 2021-09-02 09
  • レコード数は7848

• After

  • 2021-05-28 21～2021-09-02 09（毎日ではない）
  • レコード数は762744

さて、いざ尋常に......!!

各日の走行データを結合します。
後の処理のためにIDを振っておきます。

from glob import glob

path_list = glob('data/*')
new_df = pd.DataFrame()

for i, path in enumerate(path_list):
    df = pd.read_csv(path)
    df['ID'] = i
    new_df = pd.concat([new_df, df], axis=0)

new_df = new_df.reset_index(drop=True)

先ほどと同様スケーリングし、IDだけをスケーリング後のdfに結合します。
これで準備は整いました。

new_df_std = scaler(new_df, sensors)
new_df_std = pd.concat([new_df_std, new_df[['ID']]], axis=1)

dfをIDごとに抽出し、一回の走行の部分時系列(one_subsequences)を作成します。
これを全体の部分時系列(subsequences)として、結合していきます。
毎回抽出して結合しないと、まったく関係ない日の走行データ同士で部分時系列を作ってしまうので、こんな処理してます。ちょっと面倒ですね。

kmeans = KMeans(n_clusters=k, random_state=2021)
scaler = StandardScaler()

for sensor in sensors:
    subsequences = np.empty((0, window))
    for i in range(new_df_std['ID'].max()+1):
        one_df = new_df_std[new_df_std['ID']==i]
        one_subsequences = make_subsequences(one_df, sensor, window)
        subsequences = np.append(subsequences, one_subsequences, axis=0)
   
    kmeans.fit_predict(subsequences)
    centers = scaler.fit_transform(kmeans.cluster_centers_)

    plt.figure(figsize=(20,4))
    plt.title(sensor)
    plt.plot(centers[0], label='cluster1')
    plt.plot(centers[1], label='cluster2')
    plt.plot(centers[2], label='cluster3')
    plt.legend(loc='upper right')
    plt.show()

結果2

先程より全体的に平らになりましたね。
ただ、Acc_Yがかなり正弦波ぽくなりました。

面白いのがAcc_Zですね。重力の影響なのか、自転車なので段差などの影響によりノイズが多いのかわかりませんが、細かい波形になっています。

sensor	result	result2
Acc_X	正弦波ぽい	平ら
Acc_Y	あやしい	正弦波ぽい
Acc_Z	あやしい	あやしい
Roll	正弦波ぽい	平ら
Pitch	平ら	平ら
Yaw	平ら	平ら
Com_X	正弦波ぽい	平ら
Com_Y	正弦波ぽい	平ら
Com_Z	平ら	平ら

考察

今回は文献の通りk=3でクラスタリングしています。そのため、各センサにつき3パターンにグルーピングしていることになります。
果たして3パターンだけでしょうか。全体の可視化結果から見るに、3パターンよりも多そうです。
今回うまく正弦波になっていないセンサは、それが原因の可能性もあるかもしれません。

どちらにせよ、はじめにの「時系列データをsliding windowで切り取ってkmeansしてパターン見つけるみたいな手法」による特徴は、IMUでも有効ではなさそうです。

まとめ

Twitterで見かけた手法を、私が趣味で集めていた自転車の走行データ（IMU）で試してみました。
実際にいくつか正弦波ぽくなり、大変勉強になりました。
実装等で間違いがあれば、教えていただけれると幸いです。

LSTMによる時系列データの教師なし異常検知

はじめに

以前（といってもかなり前）、オートエンコーダによる時系列データの教師なし異常検知に関して記事を書きました。
今回はその続きで、同じ心電図データを用いて、LSTMによる異常検知をしたいと思います。

noleff.hatenablog.com

プログラム

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from sklearn.model_selection import train_test_split
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, LSTM

# Timeから時間の差を追加
def differ_time(df):
    # Timeから時間の差を割り当てる
    df['dif_sec'] = df['time'].diff().fillna(0)
    df['cum_sec'] = df['dif_sec'].cumsum()
    return df

# 正規化
def act_minxmax_scaler(df):
    scaler = MinMaxScaler()
    scaler.fit(df)
    # 正規化したデータをnumpyリストに
    mc_list = scaler.transform(df)

    return mc_list, scaler

# データ準備
def split_part_recurrent_data(data_list, look_back):
    X, Y = [], []
    for i in range(len(data_list)-look_back-1):
        X.append(data_list[i:(i+look_back), 0])
        Y.append(data_list[i + look_back, 0])
    
    return np.array(X), np.array(Y)

def create_lstm(look_back):
    model = Sequential()
    model.add(LSTM(4, input_shape=(look_back, 1)))
    model.add(Dense(1))

    model.compile(loss='mean_squared_error', optimizer='adam')

    return model

# LSTM学習
def act_lstm(model, train_x, train_y, batch_size, epochs):
    train_x, val_x, train_y, val_y = train_test_split(train_x, train_y, 
                                                        test_size=0.25, 
                                                        shuffle=False, 
                                                        random_state=2021)

    early_stopping = EarlyStopping(monitor='val_loss',
                                    min_delta=1.0e-3, 
                                    patience=20, 
                                    verbose=1)

    history = model.fit(train_x, train_y, 
            epochs=epochs, 
            batch_size=batch_size, 
            verbose=2,
            validation_data=(val_x, val_y), 
            callbacks=[early_stopping]
    )

    return model, history

データの読み込みから、可視化までは、オートエンコーダのときと同じです。

df = pd.read_csv('ecg.csv')

# 使うデータだけ抽出
test_df = df.iloc[:5000, :] 
train_df = df.iloc[5000:, :]

# 時間カラム追加
train_df = differ_time(train_df)
test_df = differ_time(test_df)

plt.figure(figsize=(16,4))
plt.plot(train_df['signal2'], label='Train')
plt.plot(test_df['signal2'], label='Test')
plt.legend()
plt.show()

異常の該当箇所は赤色の場所と仮定します。

anomaly_df = test_df[(test_df['cum_sec']>15)&(test_df['cum_sec']<20)]
plt.figure(figsize=(16,4))
plt.plot(anomaly_df['cum_sec'], anomaly_df['signal2'], color='tab:orange', label='Test')

anomaly_df = test_df[(test_df['cum_sec']>17)&(test_df['cum_sec']<17.5)] 
plt.plot(anomaly_df['cum_sec'], anomaly_df['signal2'], color='tab:red', label='Test')
plt.xlabel('sec')
plt.show()

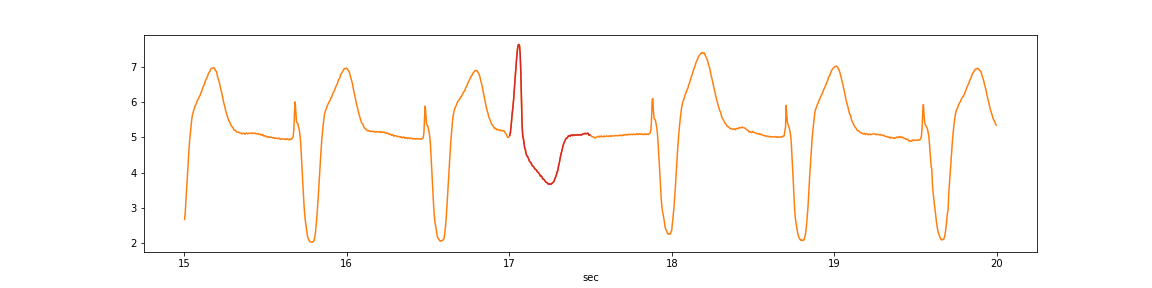
データ準備として正規化し、部分時系列にしたデータを用意します。 LSTMのデータ準備の詳細はこちらをご参考ください。
なお、look_backが250なのは、オートエンコーダの記事と合わせているだけです。

# 正規化
train_vec, train_scaler = act_minxmax_scaler(train_df[['signal2']])
test_vec, test_scaler = act_minxmax_scaler(test_df[['signal2']])

look_back = 250

train_x, train_y = split_part_recurrent_data(train_vec, look_back)
test_x, test_y = split_part_recurrent_data(test_vec, look_back)
display(pd.DataFrame(train_x))
display(pd.DataFrame(train_y))

今回、LSTMのライブラリはKerasを用います。
そのため、Kerasのお作法として、入力データを三次元にしなければりません。
そのためreshape処理をします。

# %%
print(train_x.shape)
print(test_x.shape)

# [データ数, 部分時系列数（look_back）, 特徴量数（心電の波形のみ）]へ変形
train_x = np.reshape(train_x, (train_x.shape[0], train_x.shape[1], 1))
test_x = np.reshape(test_x, (test_x.shape[0], test_x.shape[1], 1))

print(train_x.shape)
print(test_x.shape)

#(39749, 250)
#(4749, 250)
#(39749, 250, 1)
#(4749, 250, 1)

# モデル作成
model = create_lstm(look_back)
batch_size = 100
epochs = 100

# モデル学習
model, hist = act_lstm(model, train_x, train_y, batch_size, epochs)

Train on 29811 samples, validate on 9938 samples
Epoch 1/100
29811/29811 - 5s - loss: 0.0066 - val_loss: 0.0024
Epoch 2/100
29811/29811 - 3s - loss: 0.0014 - val_loss: 8.8507e-04
Epoch 3/100
29811/29811 - 3s - loss: 8.1925e-04 - val_loss: 7.0201e-04
Epoch 4/100
29811/29811 - 3s - loss: 6.6374e-04 - val_loss: 5.8554e-04
Epoch 5/100
29811/29811 - 3s - loss: 5.7173e-04 - val_loss: 5.2490e-04
Epoch 6/100
29811/29811 - 3s - loss: 5.0133e-04 - val_loss: 4.8002e-04
Epoch 7/100
29811/29811 - 3s - loss: 4.4123e-04 - val_loss: 3.9693e-04
Epoch 8/100
29811/29811 - 3s - loss: 3.9236e-04 - val_loss: 3.5257e-04
Epoch 9/100
29811/29811 - 3s - loss: 3.5195e-04 - val_loss: 3.1569e-04
Epoch 10/100
29811/29811 - 3s - loss: 3.1859e-04 - val_loss: 2.9057e-04
Epoch 11/100
29811/29811 - 3s - loss: 2.9321e-04 - val_loss: 2.6281e-04
Epoch 12/100
29811/29811 - 3s - loss: 2.7145e-04 - val_loss: 2.4727e-04
Epoch 13/100
29811/29811 - 3s - loss: 2.5357e-04 - val_loss: 2.2870e-04
Epoch 14/100
29811/29811 - 3s - loss: 2.4035e-04 - val_loss: 2.1622e-04
Epoch 15/100
29811/29811 - 3s - loss: 2.2892e-04 - val_loss: 2.1792e-04
Epoch 16/100
29811/29811 - 3s - loss: 2.2230e-04 - val_loss: 1.9697e-04
Epoch 17/100
29811/29811 - 3s - loss: 2.1219e-04 - val_loss: 1.9251e-04
Epoch 18/100
29811/29811 - 3s - loss: 2.0502e-04 - val_loss: 1.8317e-04
Epoch 19/100
29811/29811 - 2s - loss: 1.9737e-04 - val_loss: 1.7637e-04
Epoch 20/100
29811/29811 - 3s - loss: 1.8952e-04 - val_loss: 1.7019e-04
Epoch 21/100
29811/29811 - 3s - loss: 1.8515e-04 - val_loss: 1.6518e-04
Epoch 22/100
29811/29811 - 2s - loss: 1.7755e-04 - val_loss: 1.7475e-04
Epoch 00022: early stopping

予測値と実測値を比較します。
異常箇所含め、かなり予測できてるかと思います。

# 予測
test_pred = model.predict(test_x)

plt.figure(figsize=(20,4))
plt.plot(test_y)
plt.plot(test_pred)
plt.show()

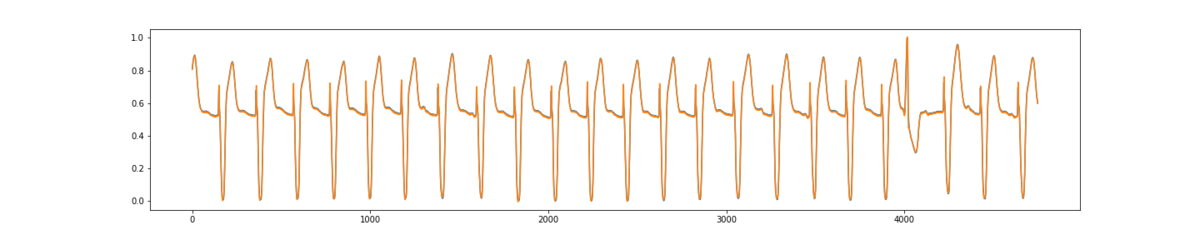
ただ、精度良く予測することではなく、異常を見つけることなので、予測値と実測値の誤差を求めます。
マハラノビス距離などもありますが、ここではユークリッド距離で計算します。

そこそこ誤検値している感が否めませんが、異常箇所が最も距離が遠くなっていることがわかるかと思います。

# 予測誤差の計算
dist = test_y - test_pred[:,0]
u_dist = pow(dist, 2)
u_dist = u_dist / np.max(u_dist)

plt.figure(figsize=(20,4))
plt.plot(test_y)
plt.plot(u_dist, color='tab:red')
plt.show()

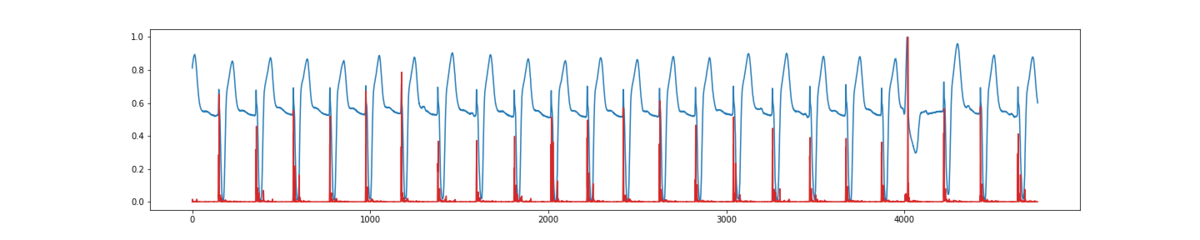
考察

心電図データに関してにはなりますが、オートエンコーダよりもLSTMの方が、明らかに精度高く予測できていることがわかりました。
しかし、異常検知で考えた場合、今回異常箇所として指定した場所のみが、うまく予測できない方が好ましい結果と言えます。
その点で言えば、オートエンコーダは異常箇所が極端に予測できなくなっているため、優れているように見えます（他のデータだと結果は変わるかもしれません）。

オートエンコーダとLSTMを組み合わせたモデルを作れば、さらに精度高く異常検知できるかもしれません。

スパイクの激しい心電図のデータはスパイクの頂点が正確に予測できていないため、LSTMは異常箇所以外も距離が遠くなって、誤検知が多くなったといえます。
これは生の心電図データだけでなく、他の特徴量を作り、それをLSTMに通せば改善されるような気もしています。

オートエンコーダによる再構成誤差とLSTMによる予測誤差を用いて異常検知する場合、どちらが良いかどうかの、メリット・デメリットは一概に言えないのが個人的見解です。
その点に関して、論文、書籍等で言及されているものがある場合、ぜひ一読したいですね。

参考文献

LSTMをよりわかりやすく＆より詳細に!<br>（前処理・世界観の説明編） - AI学習者・実務家の「疑問」を解消したい

深層学習を用いた時系列データにおける異常検知 | Kabuku Developers Blog

LSTMによる時系列データの異常検知（Keras） - Qiita

Data Mining Large Medical Time Series Databases

Google Smartphone Decimeter Challengeの解法

Google Smartphone Decimeter Challenge

概要はこちら

post-processing approach

snap to grid (snap to ground truth)

地理情報を取得し、最寄りの位置（地理情報）に予測位置を補正する手法です。
このnotebookでは、地理情報のみのアプローチですが、trainデータとtestデータで同じ経路を通っている場所も一部あることから、trainデータのground truthもsnap対象としました。

なお、最寄りの緯度経度を見つけるのは気軽に叩けないほど時間がかかりました。

Road detection and creating grid points | Kaggle

mean predict

同じ日に集めた位置情報データには、複数のスマートフォンがある含まれていることがあるため、それを平均化するアプローチです。そのまま用いました。

GSDC phones mean prediction | Kaggle

remove outlier & kalman filter

緯度経度を外れ値を線形補間し、カルマンフィルタによる平滑化をしています。 そのまま用いました（正直カルマンフィルタのパラメータ等、さっぱりわかりませんでした）。

Baseline post-processing by outlier correction | Kaggle

adaptive gauss & phone mean

ガウシアンフィルタで、緯度経度を平滑化し、複数のスマートフォンで平均化しています。
ガウシアンフィルタは、上記のremove outlier ->kalman filter よりもLBのスコアは低い印象だったため、imu approachの入力にのみ用いました。
phone meanは上記のmean predictとは違う手法だっため、こちらも採用しました。

Adaptive_gauss+phone_mean | Kaggle

moving or not

車が停止しているとき、緯度経度の精度が著しく悪くなる傾向から、車が止まっているか動いているかを判定するモデルを作成しています。
このnotebookでは、交差検証の結果94%の精度でしたが、testデータに対して可視化した結果、精度がもう少し欲しいという印象でした。
そこで、rollingで特徴量を増やし、ベースライン等の緯度経度、そのdiffなどを特徴量として加えることで98%まで精度を上げました。 ただし、PAOなどのtrainデータにはあってtestデータにはある場所は、緯度経度を特徴量として用いていることが原因なのか、正しく予測できなかったため、除外しました。

これらの結果から、停止している中で、最も時系列的に近い値で補間しました（ほとんどの方が平均で補間しており、この手法が平均補間よりも優れているという証拠があるわけではないのであしからず）。

この辺の実装はかなりギリギリでした。

A car is Moving or Not?? Accuracy 94%! | Kaggle

positon shift

スマートフォンの設置位置と車のアンテナとの差を補正するアプローチだと思っています（正直あまり見れていないです）。
こちらもギリギリで作成してみたくらいで、深く検討できなかった後処理です。

GSDC: Position shift | Kaggle

imu approach

ベースラインの緯度経度と、IMU(加速度、ジャイロ、磁気)を加えてラグ特徴量とrolling特徴量を加え、緯度経度を予測するアプローチです。 緯度経度を直接予測するのではなく、一端XYZに変換して予測していました（これが有効であるかは試していませんが、notebook投稿者いわく、緯度経度では予測がうまくいかないが、XYZではうまくできたとのことでした）。

ここからさらに精度を上げるため、ベースラインに後処理を加えた緯度経度を入力として追加しました。
具体的には以下の位置情報を入れています。

• baseline
• imu
• baseline→remove-outlier→kalman→phone-mean　 ← new!
• baseline→remove-outlier→kalman→mean-predict　 ← new!
• baseline→remove-outlier→kalman→phone-mean->mean-predict　← new!
• baseline→remove-outlier→kalman→mean-predic->phone-meant　← new!
• baseline→adaptive-gauss→phone-mean　← new!
• baseline→adaptive-gauss→mean-predict　←new!
• baseline→adaptive-gauss→phone-mean→mean-predict　← new!
• baseline→adaptive-gauss→mean-predict→phone-mean　← new!

そこから、尖度、歪度、最大ー最小などの特徴量を加え、合計約750ほどの特徴量になりました。

trainデータとtestデータにあるデータで同じ経路を通っているのは、SJCとMTVの一部でした。そのため、この手法はその部分のみ適用させました（RWCがMTVの一部と一緒だったためこれも加えています。

Predict Next Point with the IMU data | Kaggle

solution

baselineから後処理していくアプローチと、imuから後処理していくアプローチの2つから、加重平均を計算し、提出しました。
LBのスコアからimu側を重視しました（これはプラスに働いたようです）。
非常に複雑怪奇な解法な原因は、アンサンブルをするのを最後の最後まで後回しにしてしまった結果です。 最後の3、4日くらい？
imuはLBのスコアが4.2以下、baselineはLBのスコア上位3つ、という脳死選択をしてしまいました。

後処理の順番が基本同じなのは、publicLBのスコアから判断しています。ただ、これがpublicにフィッティングし過ぎた原因かもしれません。(public22位→private34位)

solution

• 補足
  • lgb：LihgtGBM
  • rf：Random Forest
  • rr：Ridge Regression

初参加のKaggleで銀メダルとるためにしたこと（Google Smartphone Decimeter Challenge）

solutionはこちら

はじめに

先日終了したGoogle Smartphone Decimeter Challenge（通称outdoorコンペ）に参加し、銀メダル（34位/810teams）をとることができました。
Kaggle初参加でしたが、相方の後輩とえっちらほっちらと蛇行しながらも、前に進めることができた結果が実ったのだと思っています。
outdoorコンペの振り返りとともに、約2ヶ月間何をしたかをまとめていきたいと思います。

www.kaggle.com

outdoorコンペ概要

スマートフォン（Android）から得られるデータから、位置（緯度・経度）を推定するコンペでした。
車にスマートフォンを固定し、データを集めるとともに、車の後部にアンテナを取り付け、それをground truthとしていました。

舞台はアメリカ、シリコンバレー！ （世界の大概のものはここにあるやん、となるらしい）

データは主に、以下のものが与えられていました。

1. GNSS関連のデータ
2. IMU関連のデータ
3. ホストが用意したベースラインとなるデータ
4. ホストが用意したGNSS関連のデータから分析しやすいように派生されたデータ

取り組み

• 毎週日曜日にミーティングをし、進捗報告
• Notionでタスク管理
• 対面以外はSlackで情報共有

6月

与えられたデータを整形し、中間データとして吐き出すプログラムを書くだけでほぼ終わりました。
本当に右も左もわからず、

「GNSSってなんだ？　GPSの親戚か？」
「ふむふむ、GNSSの中にGPSがあるのね、初知り。他にはGalileoや北斗とかあるらしい。何それかっこいい」

と初歩の初歩からさっぱりわかりませんでした。

さらに、与えられたGNSSデータのカラムもちんぷんかんぷんで、

「millisSinceGpsEpochって指つりそう……。は？　utcTimeMillis？　うるう秒？」
「これ結合しようにも、millisSinceGpsEpoch完全一致してないやん。え？　merge_asof……だと……？」

と、別ファイルにわかれているデータの時間の整合性をとることや結合自体に苦戦してました。

そんなこんなで一ヶ月があった言う間に過ぎました。
二人共、6月末と7月頭に学会発表があったということもあり、まだ全力で取り組めていなかった感がありました。

7月

このままではヤバいなとなり、Kaggle内のCodeとDiscussionを一通り漁りました。
そこで気がついたのは、後処理に関連する投稿が多かったことです。
outdoorコンペの前にindoorコンペというものがあり、そのコンペでは後処理が有効であったことから、ホストが用意したベースラインのデータをもとに、後処理をする取り組みが多くありました。

現状、ほとんど何もできていない以上、これらの後処理を実装するところから始めようとなりました。
これが7月1日の話です。

そこからは、怒涛の後処理実装と、それらをどう組み合わせるかを検討していました。
LBに投稿することで精度を比較したり、trainデータに対して後処理した結果とground truthの距離を計算し、精度向上に寄与しているかを確認したりしていました。

しかし、それらにも限界がありました。
ベースラインを主軸にしているため、ベースラインが悪ければ、どんなに後処理で補正しようにも限度というものがあります。
なお、この時点でGNSS関連の知識は依然としてゼロでした。

そこで後処理は相方に任せ、私はIMUデータのアプローチを開始しました。
IMU関連のデータは研究で扱っているため、普段から馴染みのあることもあり、さっぱりわからなかったGNSS関連のデータとにらめっこするよりも、現実的だと判断しました。
ただし、金メダルをとっている上位陣の解法をみるに、このにらめっこがなければ上位にはいけなかった、ということもまた事実です。ただ、振り返りを書いている今、この判断が間違っているとは思いません。結果論ですが。

一言で言うと、位置を推定するコンペで、GNSS関連のデータを捨てるという決断をしたことになります。

結果、IMUから位置を推定するアプローチは銅圏を出たり入ったりしていた状態から、銀圏まで一気に躍り出ることができました。

outdoor やっとこさ銅圏なので、なんとか残り一週間ほど頑張りたい

— ふる (@8_furu8) 2021年7月26日

outdoorコンペ、ラストスパートじゃぁああああああああああっ！！#kaggle pic.twitter.com/DOTFWSkQeE

— ふる (@8_furu8) 2021年8月1日

8月

はてさて、そんなこんなでラストスパート8月です。
一週間弱しかありませんでしたが、Notionにラストスパートという項目を作り、「この一週間Kaggle以外でコーディングしねぇ」くらいには気合入れてやってました。

やったことは以下になります。

1. moving or not
   車が止まっているとき精度が悪いということから、車が動いているかどうか二値分類モデルで判定し、止まっているときの緯度・経度を時系列で最も近い値で補正

2. スタッキング
   IMUから緯度経度推定をLightGBMだけでなく、ランダムフォレストとRidge回帰でも推定してスタッキング

3. アンサンブル
   IMUから推定しした緯度経度とベースラインから後処理した緯度経度の加重平均

どう考えても、時間は足りませんでした(汗)。
アンサンブルも半ば投げやりでやっていた感が否めません。
この辺りの知見はそれほどなく、本来であればLBやCVとを比較しながら検討すべき部分であるはずですが、実際LBに出せたのはラスト2日間だけでした。
ぶっちゃけ、アンサンブルするよりも、ランダムフォレスト単体の方がprivateのLBは良かったのですが、それも27、28位なので、ほぼ変わりませんでしたね。

反省点

1. 序盤（6月）はダレていた
   コンペ終了までまだ時間があると、研究を初め、Kaggle以外のことに時間を割いていました。進め方がわからず、ふわふわとしていた時間が長かったため、次Kaggleに挑戦するときは、序盤から上位に行けるよう頑張りたいところです。

2. 予定通りに進んでいない
   Notionでタスク管理するところから初めたのですが、勝手がわからず、全然予定通り進めることができませんでした。アンサンブルに時間が足りなくなったのも、予定のしわ寄せが原因です。
   アンサンブルの検証にかかる時間コストを見積もれなかったこともいけませんでした。

3. publicのLBに頼りすぎた
   publicLBでは22位でした。どのみち銀圏ですが、そこからprivateLBで34位まで落ちているので、正直publicにフィッティングし過ぎた感があります。学習系は交差検証をしていましたが、後処理系はすべて同じ順番で後処理していたため、後処理の順序を変えるなどしてバリエーション増やせば良かったのでしょうか？　

まとめ

なんとかありつけた銀メダル、でした。
東京オリンピックも日本最多メダル数ということで、どこかプレミア感があります。少なくとも初めてとったKaggleのメダルはいつか、という質問には何年経っても答えられるでしょう。（オリンピックまったく見ておりませんが）。
夏休みは研究にまたシフトするので、次にコンペ参加はいつになるやらですね。
卒業までにはもう一枚メダル取りたい気持ちはあるので、どこかで頑張りたいところです。

groupbyしてvalue_counts()したい

タイトル通りです。

データ

import pandas as pd
from sklearn.preprocessing import LabelEncoder

df = pd.DataFrame([
        ['Aさん', 100, 'S', 'cola'],
        ['Bさん', 150, 'M', 'tea'],
        ['Cさん', 200, 'L', 'tea'],
        ['Dさん', 100, 'S', 'tea'],
        ['Eさん', 200, 'L', 'coffee'],
        ['Fさん', 200, 'L', 'tea'],
        ['Gさん', 150, 'M', 'coffee'],
        ['Hさん', 200, 'L', 'coffee'],
        ['Iさん', 100, 'S', 'cola'],
        ['Jさん', 200, 'L', 'tea'],
        ['Kさん', 200, 'L', 'tea'],
        ['Lさん', 100, 'S', 'cola'],
        ['Mさん', 150, 'M', 'coffee'],
        ['Nさん', 150, 'M', 'coffee'],
        ],
        columns=['user', 'price', 'size', 'drink'])

df
#    user  price size   drink
# 0   Aさん    100    S    cola
# 1   Bさん    150    M     tea
# 2   Cさん    200    L     tea
# 3   Dさん    100    S     tea
# 4   Eさん    200    L  coffee
# 5   Fさん    200    L     tea
# 6   Gさん    150    M  coffee
# 7   Hさん    200    L  coffee
# 8   Iさん    100    S    cola
# 9   Jさん    200    L     tea
# 10  Kさん    200    L     tea
# 11  Lさん    100    S    cola
# 12  Mさん    150    M  coffee
# 13  Nさん    150    M  coffee

ラベリング

lenc = LabelEncoder()
df['drink'] = lenc.fit_transform(df['drink']) # 0=coffe, 1=cola, 2=tea
df
#    user  price size  drink
# 0   Aさん    100    S      1
# 1   Bさん    150    M      2
# 2   Cさん    200    L      2
# 3   Dさん    100    S      2
# 4   Eさん    200    L      0
# 5   Fさん    200    L      2
# 6   Gさん    150    M      0
# 7   Hさん    200    L      0
# 8   Iさん    100    S      1
# 9   Jさん    200    L      2
# 10  Kさん    200    L      2
# 11  Lさん    100    S      1
# 12  Mさん    150    M      0
# 13  Nさん    150    M      0

普通にvalue_counts()

df['drink'].value_counts()
# 2    6
# 0    5
# 1    3
# Name: drink, dtype: int64

value_counts()の最大値のindex

 # drinkで最も多いカテゴリ
df['drink'].value_counts().idxmax() # 0=coffe, 1=cola, 2=tea
# 2

平均（オーソドックスなgroupbyの使い方）

df.groupby('size').mean()[['drink']]
#          drink
# size          
# L     1.333333
# M     0.500000
# S     1.250000

groupbyしてvalue_counts()

# groupbyしてvalue_counts()
pd.DataFrame(df.groupby('size').apply(lambda df: df['drink'].value_counts().idxmax()), columns=['drink'])
#       drink
# size       
# L         2
# M         0
# S         1

以上！

複数ファイルのデータ結合方法（InvalidIndexError: Reindexing only valid with uniquely valued Index objects）

はじめに

複数ファイルにわかれたデータの結合方法のメモです。

InvalidIndexError: Reindexing only valid with uniquely valued Index objects
というエラーとも戦いました。

データ

気象庁の気象データを使いました。
広島、高松、大阪、東京、那覇の5都市分のデータです。

Pythonスクリプトと同じ階層にあるdataディレクトリの中身は以下になります。

├── data                      
│   ├── 2016               <- 2016年の気象データ
│   │   ├── 広島.csv
│   │   ├── 高松.csv
│   │   ├── 大阪.csv
│   │   ├── 東京.csv
│   ├── 2017               <- 2017年の気象データ
│   │   ├── 広島.csv
│   │   ├── 高松.csv
│   │   ├── 大阪.csv
│   │   ├── 東京.csv
│   ├── 2018               <- 2018年の気象データ
│   │   ├── 広島.csv
│   │   ├── 高松.csv
│   │   ├── 大阪.csv
│   │   ├── 東京.csv
│   ├── 2019               <- 2019年の気象データ
│   │   ├── 広島.csv
│   │   ├── 高松.csv
│   │   ├── 大阪.csv
│   │   ├── 東京.csv
│   │   ├── 那覇.csv

dataを表にするとこんな感じです。

data

結合方法

以下の1と2の方法があるかと思います。
今回はどちらが良いかの議論はしませんが、ケースバイケースな気がします。
1で本記事は進めます。

1. merge→concat

   

   merge→concat

2. concat→merge

   

   concat→merge

結合手順

手始めに

まず、データをロードするために、ファイルのパスを取得します。

# %%
import pandas as pd
import numpy as np
import glob as gb
from IPython.core.display import display

# %%
# カラムを表示
def print_columns(df):
    for col in df.columns:
        print(col)

# %%
# データパス
path2016_list = gb.glob('data/2016/*.csv')
path2017_list = gb.glob('data/2017/*.csv')
path2018_list = gb.glob('data/2018/*.csv')
path2019_list = gb.glob('data/2019/*.csv')

2016年だけとりあえず結合してみます。

merge

# %%
# 雑に2016だけ
print(path2016_list)
# ['data/2016\\大阪.csv', 'data/2016\\広島.csv', 'data/2016\\東京.csv', 'data/2016\\高松.csv']

hiroshima_df = pd.read_csv(path2016_list[0])
osaka_df = pd.read_csv(path2016_list[1])
takamatsu_df = pd.read_csv(path2016_list[2])
tokyo_df = pd.read_csv(path2016_list[3])

display(hiroshima_df.head())
display(osaka_df.head())
display(takamatsu_df.head())
display(tokyo_df.head())

各都市の気象データ

3回結合します。
このとき、カラムが重複するという問題が発生します。

# %%
# merge①
df = pd.merge(hiroshima_df, osaka_df, on=['年', '月', '日'])
print_columns(df)

# 年
# 月
# 日
# 曜日_x
# 平均気温_x
# 最高気温_x
# 最高気温時間_x
# 最低気温_x
# 最低気温時間_x
# 降水量の合計_x
# 平均雲量_x
# 平均風速_x
# 平均湿度_x
# 曜日_y
# 平均気温_y
# 最高気温_y
# 最高気温時間_y
# 最低気温_y
# 最低気温時間_y
# 降水量の合計_y
# 平均雲量_y
# 平均風速_y
# 平均湿度_y

# merge②
df = pd.merge(df, takamatsu_df, on=['年', '月', '日'])
print_columns(df)

# 年
# 月
# 日
# 曜日_x
# 平均気温_x
# 最高気温_x
# 最高気温時間_x
# 最低気温_x
# 最低気温時間_x
# 降水量の合計_x
# 平均雲量_x
# 平均風速_x
# 平均湿度_x
# 曜日_y
# 平均気温_y
# 最高気温_y
# 最高気温時間_y
# 最低気温_y
# 最低気温時間_y
# 降水量の合計_y
# 平均雲量_y
# 平均風速_y
# 平均湿度_y
# 曜日
# 平均気温
# 最高気温
# 最高気温時間
# 最低気温
# 最低気温時間
# 降水量の合計
# 平均雲量
# 平均風速
# 平均湿度

# merge③
df = pd.merge(df, takamatsu_df, on=['年', '月', '日'])
print_columns(df)

# 年
# 月
# 日
# 曜日_x
# 平均気温_x
# 最高気温_x
# 最高気温時間_x
# 最低気温_x
# 最低気温時間_x
# 降水量の合計_x
# 平均雲量_x
# 平均風速_x
# 平均湿度_x
# 曜日_y
# 平均気温_y
# 最高気温_y
# 最高気温時間_y
# 最低気温_y
# 最低気温時間_y
# 降水量の合計_y
# 平均雲量_y
# 平均風速_y
# 平均湿度_y
# 曜日_x
# 平均気温_x
# 最高気温_x
# 最高気温時間_x
# 最低気温_x
# 最低気温時間_x
# 降水量の合計_x
# 平均雲量_x
# 平均風速_x
# 平均湿度_x
# 曜日_y
# 平均気温_y
# 最高気温_y
# 最高気温時間_y
# 最低気温_y
# 最低気温時間_y
# 降水量の合計_y
# 平均雲量_y
# 平均風速_y
# 平均湿度_y

③で重複が発生しているのがわかります。

そもそも、_x、_yは何なのか

これはpd.mergeメソッドの引数suffixesのデフォルト値です。
重複するとxとyとつけるようになっています。
しかし、同じカラムのあるデータを3回結合すると、重複は再び起きます。

これを回避するのが本記事の目的です。

各都市でやる

# %%
def load_df(paths):
    allcity_df = pd.read_csv(paths[0])
    for path in paths[1:]:
        oneyear_df = pd.read_csv(path)
        allcity_df = pd.merge(allcity_df, oneyear_df, on=['年', '月', '日'])
    
    return allcity_df

# %%
# ロード
df_2016 = load_df(path2016_list)
df_2017 = load_df(path2017_list)
df_2018 = load_df(path2018_list)
df_2019 = load_df(path2019_list)

もちろん、同じ問題が起きます。

# %%
print_columns(df_2016)
# 年
# 月
# 日
# 曜日_x
# 平均気温_x
# 最高気温_x
# 最高気温時間_x
# 最低気温_x
# 最低気温時間_x
# 降水量の合計_x
# 平均雲量_x
# 平均風速_x
# 平均湿度_x
# 曜日_y
# 平均気温_y
# 最高気温_y
# 最高気温時間_y
# 最低気温_y
# 最低気温時間_y
# 降水量の合計_y
# 平均雲量_y
# 平均風速_y
# 平均湿度_y
# 曜日_x
# 平均気温_x
# 最高気温_x
# 最高気温時間_x
# 最低気温_x
# 最低気温時間_x
# 降水量の合計_x
# 平均雲量_x
# 平均風速_x
# 平均湿度_x
# 曜日_y
# 平均気温_y
# 最高気温_y
# 最高気温時間_y
# 最低気温_y
# 最低気温時間_y
# 降水量の合計_y
# 平均雲量_y
# 平均風速_y
# 平均湿度_y

問題点

カラムが重複すると何が問題でしょうか。
今回は二つの例で示します。

1. 一度に二つのカラムが触れてしまう

単に出力しても、計算しても、代入しても全部二つのカラムを指定してしまいます。

df_2016['平均気温_x'].head()

#    平均気温_x  平均気温_x
# 0       7.6       7.5
# 1       8.1       7.3
# 2      10.9       9.3
# 3      11.2       9.2
# 4      10.0      10.9

2. concatするとエラー

merge→concatで結合する今回は、mergeした各都市のデータを年ごとにconcatしなければなりません。
そのとき、カラムが重複しているエラーが出ます。
それがInvalidIndexError: Reindexing only valid with uniquely valued Index objectsです。

【再掲】merge→concat

concat①、concat②の時点でもカラムは重複していますが、カラムが完全一致していたため、エラーが出ることなく結合できていたようです。
しかし、2019年だけに那覇の気象データがあるような（データがある時から増えるようなケースが往々にしてあるという前提）場合において、カラムが完全一致しないため、上記のエラーが出るようです。

# %%
# concat① (2016と2017の結合)
concated_df = pd.concat([df_2016, df_2017], axis=0, ignore_index=True)
print_columns(concated_df)

# 年
# 月
# 日
# 曜日_x
# 平均気温_x
# 最高気温_x
# 最高気温時間_x
# 最低気温_x
# 最低気温時間_x
# 降水量の合計_x
# 平均雲量_x
# 平均風速_x
# 平均湿度_x
# 曜日_y
# 平均気温_y
# 最高気温_y
# 最高気温時間_y
# 最低気温_y
# 最低気温時間_y
# 降水量の合計_y
# 平均雲量_y
# 平均風速_y
# 平均湿度_y
# 曜日_x
# 平均気温_x
# 最高気温_x
# 最高気温時間_x
# 最低気温_x
# 最低気温時間_x
# 降水量の合計_x
# 平均雲量_x
# 平均風速_x
# 平均湿度_x
# 曜日_y
# 平均気温_y
# 最高気温_y
# 最高気温時間_y
# 最低気温_y
# 最低気温時間_y
# 降水量の合計_y
# 平均雲量_y
# 平均風速_y
# 平均湿度_y

# %%
# concat② (上記dfと2018の結合)
concated_df = pd.concat([concated_df, df_2018], axis=0, ignore_index=True)
print_columns(concated_df)
# concat① (2016と2017の結合)と同じ結果


# %%
# concat③ (上記dfと2019の結合)
# エラー
concated_df = pd.concat([concated_df, df_2019], axis=0, ignore_index=True)
# InvalidIndexError: Reindexing only valid with uniquely valued Index objects

重複していない場合

簡単なデータで重複していないときのconcatの挙動を見てみます。
こちらを参考にコードを作成しました。
データがない箇所はNaNになり、問題なく結合自体はできていることがわかるかと思います。

# %%
# かぶってなかったらエラーにならない
df1 = pd.DataFrame({'A': ['A1', 'A2', 'A3'],
                    'B': ['B1', 'B2', 'B3'],
                    'C': ['C1', 'C2', 'C3']})
print(df1)
#       A   B   C
# 0    A1  B1  C1
# 1    A2  B2  C2
# 2    A3  B3  C3

# %%
df2 = pd.DataFrame({'A': ['A1', 'A2', 'A3'],
                    'B': ['B1', 'B2', 'B3'],
                    'C': ['C2', 'C3', 'C4'],
                    'D': ['D2', 'D3', 'D4']})
print(df2)
#     A   B   C   D
# 0  A1  B1  C2  D2
# 1  A2  B2  C3  D3
# 2  A3  B3  C4  D4

# %%
df_concat = pd.concat([df1, df2], axis=0, ignore_index=True)

print(df_concat)
#     A   B   C    D
# 0  A1  B1  C1  NaN
# 1  A2  B2  C2  NaN
# 2  A3  B3  C3  NaN
# 3  A1  B1  C2   D2
# 4  A2  B2  C3   D3
# 5  A3  B3  C4   D4

改良版の作成

先程のload_df関数を改良します。
ただ、問題はこの改良方法がコード的に美しくない（少々強引）ことです。
他に良い案があれば、是が非でもご教示していただきたく……。

アイデアはデータを辞書に入れることと、その辞書のkeyを引数suffixesに指定することです。

# %%
# load_dfを改良
def load2_df(paths):
    city_names = {'広島', '大阪', '那覇', '高松', '東京'}
    df_dict = make_df_dict(paths, city_names)
    
    allcity_df = df_dict['広島']
    df_dict.pop('広島')
    for city in df_dict.keys():
        allcity_df = pd.merge(allcity_df, df_dict[city], 
                            on=['年', '月', '日'],
                            suffixes=('', f'_{city}'))
    
    return allcity_df

# 各都市のデータを辞書に入れる
def make_df_dict(paths, city_names):
    df_dict = {}
    for path in paths:
        for city in city_names:
            if city in path:
                df_dict[city] = pd.read_csv(path)
    
    return df_dict

# %%
# ロード2(改良版)
df2_2016 = load2_df(path2016_list)
df2_2017 = load2_df(path2017_list)
df2_2018 = load2_df(path2018_list)
df2_2019 = load2_df(path2019_list)

# %%
print_columns(df2_2016)
# 年
# 月
# 日
# 曜日
# 平均気温
# 最高気温
# 最高気温時間
# 最低気温
# 最低気温時間
# 降水量の合計
# 平均雲量
# 平均風速
# 平均湿度
# 曜日_大阪
# 平均気温_大阪
# 最高気温_大阪
# 最高気温時間_大阪
# 最低気温_大阪
# 最低気温時間_大阪
# 降水量の合計_大阪
# 平均雲量_大阪
# 平均風速_大阪
# 平均湿度_大阪
# 曜日_東京
# 平均気温_東京
# 最高気温_東京
# 最高気温時間_東京
# 最低気温_東京
# 最低気温時間_東京
# 降水量の合計_東京
# 平均雲量_東京
# 平均風速_東京
# 平均湿度_東京
# 曜日_高松
# 平均気温_高松
# 最高気温_高松
# 最高気温時間_高松
# 最低気温_高松
# 最低気温時間_高松
# 降水量の合計_高松
# 平均雲量_高松
# 平均風速_高松
# 平均湿度_高松

# %%
print_columns(df2_2017)
# df2_2016と同じ

# %%
print_columns(df2_2018)
# df2_2016と同じ

# %%
print_columns(df2_2019)
# 年
# 月
# 日
# 曜日
# 平均気温
# 最高気温
# 最高気温時間
# 最低気温
# 最低気温時間
# 降水量の合計
# 平均雲量
# 平均風速
# 平均湿度
# 曜日_大阪
# 平均気温_大阪
# 最高気温_大阪
# 最高気温時間_大阪
# 最低気温_大阪
# 最低気温時間_大阪
# 降水量の合計_大阪
# 平均雲量_大阪
# 平均風速_大阪
# 平均湿度_大阪
# 曜日_東京
# 平均気温_東京
# 最高気温_東京
# 最高気温時間_東京
# 最低気温_東京
# 最低気温時間_東京
# 降水量の合計_東京
# 平均雲量_東京
# 平均風速_東京
# 平均湿度_東京
# 曜日_那覇
# 平均気温_那覇
# 最高気温_那覇
# 最高気温時間_那覇
# 最低気温_那覇
# 最低気温時間_那覇
# 降水量の合計_那覇
# 平均雲量_那覇
# 平均風速_那覇
# 平均湿度_那覇
# 曜日_高松
# 平均気温_高松
# 最高気温_高松
# 最高気温時間_高松
# 最低気温_高松
# 最低気温時間_高松
# 降水量の合計_高松
# 平均雲量_高松
# 平均風速_高松
# 平均湿度_高松

2019年にしかない那覇も問題なくできました。

広島は？

_都市名となっていないデータが広島であることは、コードを書いた本人（私）しかわかりません。
これも強引に後処理を書くとこんな感じでしょうか。

# %%
# しいて書くならの後処理
columns = ['曜日', '平均気温', '最高気温', '最高気温時間'
        '最低気温', '最低気温時間', '降水量の合計',
        '平均雲量', '平均風速', '平均湿度']

for col in columns:
    df2_2019 = df2_2019.rename(columns={col: f'{col}_広島'})

# %%
print_columns(df2_2019)
# 年
# 月
# 日
# 曜日_広島
# 平均気温_広島
# 最高気温_広島
# 最高気温時間
# 最低気温
# 最低気温時間_広島
# 降水量の合計_広島
# 平均雲量_広島
# 平均風速_広島
# 平均湿度_広島
# 曜日_大阪
# 平均気温_大阪
# 最高気温_大阪
# 最高気温時間_大阪
# 最低気温_大阪
# 最低気温時間_大阪
# 降水量の合計_大阪
# 平均雲量_大阪
# 平均風速_大阪
# 平均湿度_大阪
# 曜日_東京
# 平均気温_東京
# 最高気温_東京
# 最高気温時間_東京
# 最低気温_東京
# 最低気温時間_東京
# 降水量の合計_東京
# 平均雲量_東京
# 平均風速_東京
# 平均湿度_東京
# 曜日_那覇
# 平均気温_那覇
# 最高気温_那覇
# 最高気温時間_那覇
# 最低気温_那覇
# 最低気温時間_那覇
# 降水量の合計_那覇
# 平均雲量_那覇
# 平均風速_那覇
# 平均湿度_那覇
# 曜日_高松
# 平均気温_高松
# 最高気温_高松
# 最高気温時間_高松
# 最低気温_高松
# 最低気温時間_高松
# 降水量の合計_高松
# 平均雲量_高松
# 平均風速_高松
# 平均湿度_高松

おわりに

複数ファイルのデータ結合方法について直面した問題をまとめました。
もっとスマートに書けないもんか。

参考文献

気象庁|過去の気象データ・ダウンロード

pandas.DataFrame, Seriesを連結するconcat | note.nkmk.me